The Nobel Prize in Physics for 2004 Announced

Posted on: Oct 7, 2004

David J. Gross
Kavli Institute for Theoretical Physics, University of California, Santa Barbara, USA,

H. David Politzer
California Institute of Technology (Caltech), Pasadena, USA, and

Frank Wilczek
Massachusetts Institute of Technology (MIT), Cambridge, USA.

Image courtesy: Nobelprize.org

The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Physics for 2004 'for the discovery of asymptotic freedom in the theory of the strong interaction' jointly to

David J. Gross
Kavli Institute for Theoretical Physics, University of California, Santa Barbara, USA,

H. David Politzer
California Institute of Technology (Caltech), Pasadena, USA, and

Frank Wilczek
Massachusetts Institute of Technology (MIT), Cambridge, USA.

A 'colourful' discovery in the world of quarks

What are the smallest building blocks in Nature? How do these particles build up everything we see around us? What forces act in Nature and how do they actually function?

This year's Nobel Prize in Physics deals with these fundamental questions, problems that occupied physicists throughout the 20th century and still challenge both theoreticians and experimentalists working at the major particle accelerators.

David Gross, David Politzer and Frank Wilczek have made an important theoretical discovery concerning the strong force, or the 'colour force' as it is also called. The strong force is the one that is dominant in the atomic nucleus, acting between the quarks inside the proton and the neutron. What this year's Laureates discovered was something that, at first sight, seemed completely contradictory. The interpretation of their mathematical result was that the closer the quarks are to each other, the weaker is the 'colour charge'. When the quarks are really close to each other, the force is so weak that they behave almost as free particles. This phenomenon is called ”asymptotic freedom”. The converse is true when the quarks move apart: the force becomes stronger when the distance increases. This property may be compared to a rubber band. The more the band is stretched, the stronger the force.

This discovery was expressed in 1973 in an elegant mathematical framework that led to a completely new theory, Quantum ChromoDynamics, QCD. This theory was an important contribution to the Standard Model, the theory that describes all physics connected with the electromagnetic force (which acts between charged particles), the weak force (which is important for the sun's energy production) and the strong force (which acts between quarks). With the aid of QCD physicists can at last explain why quarks only behave as free particles at extremely high energies. In the proton and the neutron they always occur in triplets.

Thanks to their discovery, David Gross, David Politzer and Frank Wilczek have brought physics one step closer to fulfilling a grand dream, to formulate a unified theory comprising gravity as well – a theory for everything.

The discovery which is awarded this year's Nobel Prize is of decisive importance for our understanding of how the theory of one of Nature's fundamental forces works, the force that ties together the smallest pieces of matter – the quarks. David Gross, David Politzer and Frank Wilczek have through their theoretical contributions made it possible to complete the Standard Model of Particle Physics, the model that describes the smallest objects in Nature and how they interact. At the same time it constitutes an important step in the endeavour to provide a unified description of all the forces of Nature, regardless of the spatial scale – from the tiniest distances within the atomic nucleus to the vast distances of the universe.

The strong force explained

The strong interaction – often called the colour interaction – is one of Nature’s four basic forces. It acts between the quarks, the constituents that build protons, neutrons and the nuclei. Progress in particle physics or its relevance for our daily life can sometimes appear hard to grasp for anyone without a knowledge of physics. However, when analysing an everyday phenomenon like a coin spinning on a table, its movements are in fact determined by the fundamental forces between the basic building blocks – protons, neutrons, electrons. In fact, about 80% of the coin’s weight is due to movements and processes in the interior of the protons and neutrons – the interaction between quarks. This year’s Nobel Prize is about this interaction, the strong or colour force.

David Gross, David Politzer and Frank Wilczek discovered a property of the strong inter­action which explains why quarks may behave almost as free particles only at high energies. The discovery laid the foundation for the theory for the colour interaction (a more complete name is Quantum ChromoDynamics, QCD). The theory has been tested in great detail, in particular during recent years at the European Laboratory for Particle Physics, CERN, in Geneva.

The Standard Model and the four forces of Nature

The first force that must have been evident to humans is gravity. This is the interaction that makes objects fall to the ground but also governs the movements of planets and galaxies. Gravity may seem strong – consider, for example, the large craters formed by comets hitting the earth, or the huge rockets that are required to lift a satellite into space. However, in the microcosmos, among particles like electrons and protons, the force of gravity is extremely weak (fig.1).

The three forces or interactions, as phycisists prefer to call them, that are applicable to the microcosmos are described by the Standard Model. They are the electromagnetic interaction, the weak interaction and the strong interaction. Through the contributions of several earlier Nobel Laureates the Standard Model has a very strong theoretical standing. This is because it is the only mathematical description which takes into account both Einstein’s theory of relativity and quantum mechanics.

The Standard Model describes quarks, leptons and force-carrying particles. Quarks build, for instance, the protons and neutrons of the atomic nucleus. Electrons that form the outer casing for atoms are leptons and, as far as is known, are not constructed from any smaller constituents. The atoms join up to form molecules, the molecules build up structures and in this way the whole universe can finally be described.

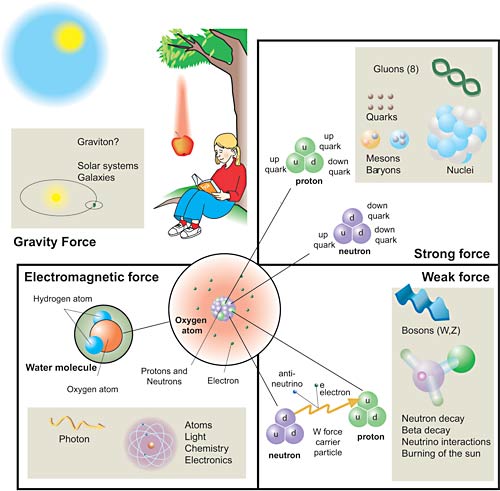
Fig. 1. The four forces (or interactions) of Nature, their force carrying particles and the phenomena or particles affected by them. The three interactions that govern the microcosmos are all much stronger than gravity and have been unified through the Standard Model.

The electromagnetic interaction provides light and cohesion

The electromagnetic interaction is responsible for a number of common phenomena in the world that surrounds us, such as friction, magnetism and the fact that neither we nor objects we lay aside fall through the floor.

The electromagnetic interaction that binds an electron and a proton in a hydrogen atom is the inconceivably large number of 1041 times stronger than gravity. Yet, in spite of the very large difference in strength between the two interactions there are several similarities. The interaction strength decreases with the square of the distance and has a long range. Both the electromagnetic interaction and the gravitational interaction are mediated by force carriers, the graviton and the photon (the light particle). In contrast to the photon, the graviton still hasn’t been found. Their long range can be shown to be due to the fact that they have no rest mass. The photons from the sun are necessary for life on earth. However, when the energy is produced from fusion at the centre of the sun the other two interactions in the Standard Model also play important roles. The photon has an important property; it is electrically neutral but couples with electrical charges. That is why photons do not interact with each other.

The electromagnetic interaction is described by the theory of quantum electrodynamics (QED), one of the most successful theories of physics. It agrees with the results of experiments with a precision that approaches one part in ten million. Sin-itiro Tomonaga, Julian Schwinger and Richard Feynman were awarded the Nobel Prize for this in 1965. One of the reasons why it is so successful is that the equation contains a small constant, the so-called fine structure constant or coupling constant, aem, with the value of 1/137, which is considerably smaller than 1. This makes it possible to calculate electromagnetic effects as a series expansion in the small constant, an elegant mathematical method called perturbation calculation that was much developed by Feynman.

One important property of quantum mechanics in the QED theory is that the fine structure constant could be shown to vary with energy; it increases with increasing energy. At today’s accelerators, for example the CERN LEP accelerator, the value has been measured as 1/128 rather than 1/137 at energies corresponding to approximately 100 billion electronvolts. If the energy dependence for the fine structure constant is depicted in relation to the energy, the curve slopes slightly upwards. Theoretical physicists say that the derivate, or the beta function, is positive.

The weak interaction – radioactive decay

The weak interaction is carried by the bosons, W± and Z0, particles that, unlike the photon and the graviton, have very large masses (approximately 100 proton masses!). That is why the interaction has a short range. It acts on both quarks and leptons and is responsible for some radioactive decays. It is closely related to the electromagnetic interaction and the two interactions are said to be united in the electroweak interaction, which was elucidated in the 1970s. Gerardus ’t Hooft and Martinus Veltman received the 1999 Nobel Prize for the final formulation of this theory.

The strong interaction – charge and colour

It had been known since the 1960s that the proton (and the neutron) are composite and built up of quarks. However, strangely enough, it was not possible to produce free quarks. They are confined, a fundamental property of these building blocks. Only aggregates of quarks, two or three, can exist freely as, for example, the proton. Quarks have electric charges which are a fraction of the proton’s, –1/3 or +2/3, a strange feature which has not yet been explained. Each quark, in addition to an electric charge, also has a special property which, like its electric charge, is quantised, that is, it can only take on certain values. This property is called colour charge, owing to its similarity to the concept of colour.

Quarks can carry the colour charges red, blue or green. For every quark there is an antiquark in the same way as the electron has an antiparticle, the positron. Antiquarks have the colour charges antired, antiblue or antigreen. Aggregates of quarks, which can exist freely, are colour neutral. The three quarks in the proton (u, u and d) have different colour charges so that the total colour charge is white (or neutral). In the same way as electrically neutral molecules can form bonds (through the attraction between their positive and negative parts) the exchange of force between protons and neutrons in the nucleus occurs through the colour forces that leak out from their quarks and force-carrying particles.

The force between quarks is carried by gluons (from the word ‘glue’), which, like photons, lack mass. Gluons, however, in contrast to photons, also have the property of colour charge, consisting of a colour and an anticolour. This property is what makes the colour force so complex and different from the electromagnetic force.

A weaker coupling sets the particles free

For a long time physicists believed that it would be impossible to find a theory by which the effects of the strong interaction between quarks could be calculated in the same way as for the electromagnetic or the weak interaction. If, for example, the interaction between two protons in a nucleus is studied, quite good results can be obtained by describing it as an exchange of pi-mesons – an idea that gave Hideki Yukawa the Nobel Prize in 1949. A coupling constant larger than 1 is needed, however, which means that Feynman’s perturbation calculations (see above) cannot be used. Unfortunately, even today there is no satisfactory method for calculating such strong interaction effects.

The situation seemed to be even worse for higher energies; if the beta function is positive (the way the coupling constant changes with energy) the interaction will be even stronger and the calculations become increasingly absurd.

The German theoretical physicist, Kurt Symanzik (now deceased), realised that the only way to achieve a reasonable theory was to find one with a negative beta function. That would also explain why quarks could sometimes appear as free particles, grains, inside the proton – an effect that had been seen in scattering experiments between electrons and protons.

Unfortunately, Symanzik himself did not find such a theory, and although Gerardus ’t Hooft was very close to discovering it during the summer of 1972, physicists started to despair. “Evidence” was even presented that all realistic theories had a positive beta function. We now know it was incorrect because in June 1973 this year’s Laureates entered the arena. In two publications back-to-back in the journal Physical Review Letters, one by Gross and Wilczek and one by Politzer, the amazing discovery was announced that the beta function can be negative. When their discovery was made, these physicists were quite young – Wilczek and Politzer were still graduate students, in fact.

According to their theories, the force carriers, the gluons, have a unique and highly unexpected property, namely that they interact not only with quarks but also with each other. This property means that the closer quarks come to each other, the weaker the quark colour charge and the weaker the interaction. Quarks come closer to each other when the energy increases, so the interaction strength decreases with energy. This property, called asymptotic freedom, means that the beta function is negative. On the other hand, the interaction strength increases with increasing distance, which means that a quark cannot be removed from an atomic nucleus. The theory confirmed the experiments: quarks are confined, in groups of three, inside the proton and the neutron but can be visualized as “grains” in suitable experiments.

Asymptotic freedom makes it possible to calculate the small distance interaction for quarks and gluons, assuming that they are free particles. By colliding the particles at very high energies it is possible to bring them close enough together. When asymptotic freedom had been discovered and a theory, Quantum ChromoDynamics, QCD, that was asymptomatically free, had been formulated, calculations could be made for the first time that showed excellent agreement with experiments (fig. 2).

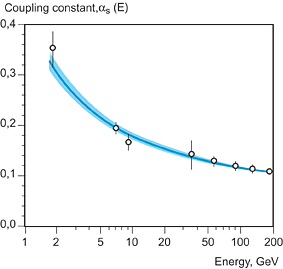
Fig. 2. The value of the “running” coupling constant, as, as a function of the energy scale E. The curve that slopes downwards (negative beta function) is a prediction of the asymptomatic freedom in QCD and, as can be seen, it agrees very closely with the measurements that have been made.

The showers of particles reveal the truth

An important proof of the QCD theory is provided by the collisions between electrons and their antiparticles, positrons, with very high kinetic energy, when they annihilate each other. According to Einstein’s equation E=mc2, kinetic energy can be transformed into new particles, for example, quarks with mass and kinetic energy. These quarks are created very deep within the process, very close to each other but moving away from each other at an extremely high speed. Thanks to the asymptotic freedom in QCD it is now possible to calculate this process.

Admittedly, when the quarks have moved away from each other, they are influenced by increasingly strong forces that eventually lead to the creation of new quark-antiquark particles, and a shower of particles arises in the direction of the original quarks and antiquarks respectively. But the process retains a “memory” of the first asymptomatically free part which can be calculated, giving a value for the probability of the occurrence of these two-shower events that agrees with observations.

Even more convincing, perhaps, are the three-shower occurrences discovered at the DESY accelerator in Hamburg in the late 1970s. These occurrences can be successfully interpreted as a gluon radiating away from a quark or an antiquark (fig. 3).

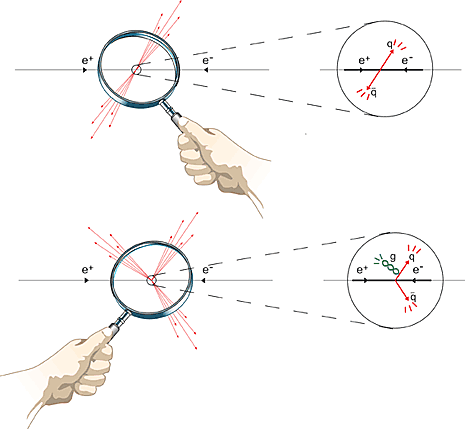
Fig. 3. Occurrences of two or three showers of particles observed in collisions between electrons and positrons. The enlarged portion displays the QCD interpretation, that also allows detailed calculations of the probability for these occurrences. These probabilities agree very well with measured data (e–= electron, e+= positron, q= quark, q with overscore= antiquark, g= gluon).

The QCD asymptotic freedom that this year's Laureates discovered also provided physicists with an explanation of a phenomenon that had been observed several years earlier at the Stanford accelerator (Friedman, Kendall and Taylor; Nobel Prize in 1990). The electrically-charged constituents of the proton behave as free particles when they are hit so hard that they get a high energy. By adding together the amount of the proton’s momentum that comprised the charged constituents (the quarks) it also became evident that about half of the proton momentum was something else – gluons!

Can the forces of Nature be unified?

Perhaps the most tantalizing effect of QCD asymptotic freedom is that it opens up the possibility of a unified description of Nature’s forces. When examining the energy dependence of the coupling constants for the electromagnetic, the weak and the strong interaction, it is evident that they almost, but not entirely, meet at one point and have the same value at a very high energy. If they do indeed meet at one point, it may be assumed that the three interactions are unified, an old dream of physicists, who would like to describe the laws of Nature in the simplest language possible (fig. 4).

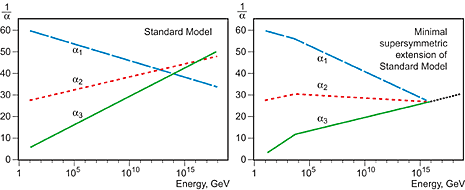
Fig. 4. Running coupling constants in the Standard Model (left) and with the introduction of supersymmetry (right). In the Standard Model the three lines, which show the inverse value of the coupling constant for the three fundamental forces, do not meet at one point, but with the introduction of supersymmetry, and assuming that the supersymmetric particles are not heavier than about 1 TeV/c2, they do meet at one point. Is this an indication that supersymmetry will be discovered at the next accelerator at CERN, the Large Hadron Collider, or is it merely a coincidence?

However, the Standard Model needs some modification if the dream of the unification of the forces of Nature is to be realised. One possibility is to introduce a new set of particles, supersymmetric particles, that may have a small enough mass to be investigated at the LHC accelerator that is now being built at CERN in Geneva.

If supersymmetry is discovered, it will also imply strong support for string theories that may even unify gravitation with the other three interactions. The Standard Model also needs modification to incorporate the recently discovered properties of neutrinos - that they have a mass different from zero. In addition, perhaps this will lead to an explanation of a number of other cosmological enigmas such as the dark matter that seems to dominate space. Regardless of this development, it is clear that the fantastic and unexpected discovery of asymptotic freedom in QCD (fig. 5) has profoundly changed our understanding of the ways in which the basic forces of Nature in our world work.

< Back to more news